メモ：ギブスサンプリングはメトロポリス・ヘイスティングス法の特殊な場合． « 谷口忠大HomePage (たにちゅーのＨＰ)

メモ：ギブスサンプリングはメトロポリス・ヘイスティングス法の特殊な場合．

2012-03-21 (wed)｜カテゴリー：

｜

ちらちら見ていたこの事実をあまりちゃんと納得していなかった．

最近メトロポリス・ヘイスティングス法を使う事がでてきたので

抑えておかねばと．

は上記 wikipediaでご理解いただくとして，

提案分布

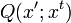
$\displaystyle Q(x'; x^t )$

を用いて現在のサンプルから，次のサンプルを提案していく．

サンプルの確率が増大すれば，サンプルを採択し，また，低下すると下式右辺の確率で

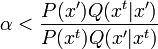
$\alpha < \frac{P(x')Q(x^t|x')}{P(x^t)Q(x'|x^t)} \,\!$

採択するというもの．（αは [0,1]一様乱数からサンプルすればよい）

ギブスサンプリングは，一変数以外を固定して，その一変数のための事後確率分布を用いて

サンプリングしていくものだが，特に採択とかそういうことがない．

なんとなく，腑に落ちていなかってほったらかしていたんですが（ごめんなさい）

ちょっと調べたらわかった．

（↑一部受理確率の式に誤記があるので注意）

提案分布Qに対象の変数の事後確率分布を用いると，綺麗に式がキャンセルされて，

１になるんですね．

ですから，αによらず，常に採択されるというロジックらしいです．

なるほど．

まさに，特殊な場合ですね．

MCMC歴２年．初学者モードですみません・・・・．(^_^)

@tanichuをフォロー

tanichuの著作