Shared Segmentation of Natural Scenes Using Dependent Pitman-Yor Process のメモ
一昨年くらいに,今はNAISTに言ったK君に紹介してもらった論文.
今から考えるとお恥ずかしい話なのですが,当時はGaussian Process をよくわかっておらず,
その時は意味をとることができませんでした.今なら,ワカル!!!!
ってことで NIPS ‘08 の論文です.
著者は
Erik B. Sudderth and Michael I. Jordan
でいつもながら,ジョーダン研ですね.
ホントにこのラボは凄いですね.
ちなみに,Erik B. Sudderth さんは, 僕がここ2,3年よく使っている.
E. Fox の sticky HDP-HMM の共著者というところでも,認識しています.
本論文は, Segmentation of Natural Scenes ということで,
自然画像の領域分割を扱っています.
複雑なように見えて,意外と素直なアプローチに思えたので,良いと思います.
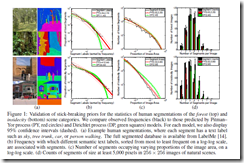
まず,第一歩として,写真の領域を人手でくくって,名前をつけたデータに対して,
そのラベルと,生起頻度がべき乗則を満たしているということを指摘します.
このあたり,よく考えると,自然言語文の単語生起そのもので面白いですね.
ゆえに,その頻度をモデル化するのにDPよりも Pitman-Yor 過程がいいだろう.という主張になっています.
# ただ,本件については,どこまで本質的かは,私は判断つかない.
次に,画像の領域分割の生成モデルを与えます.
3章でシンプルなBags of image features モデルを導入します.
基本的には,super pixcel 毎にtexture color のカテゴリが対応して,そこから多項分布で
生成される.というモデル.
LDAのセンスそのまま.
しかしながら,このようなモデルだと,空間的な連続性を与えられない.という話が出てきます.
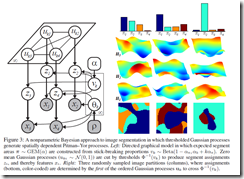
そこで,4章にて 裏に,GPを走らせて,空間分割をやろうという.
Spatially Dependent Pitman-Yor Process の考え方があらわれます.
どうもこのあたりのアイデアは, [24] J.A. Duan 2007 のアイデアっぽいのですが,非常にセンスが良いように感じました.
おもしろい.
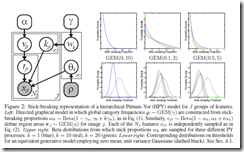
まず,sticky breaking-process が[0,1] 区間の値による,棒の切れ端の切断の繰り返しだということを思い出します.
通常,その切断はBeta 分布でやるんですが,ここでは,Gauss分布を上手く使うことによって,実現します.
それは,Gauss分布の累積分布関数(CDF)を持ってきます.そこで,vという確率に達する変数をu=Φ^{-1}(v) として計算できるようにします.結局このCDFの逆関数を介せば,0 or 1 の値を出す,関数がGauss をバックに構成できるわけです.
(4)式は地味にけっこうキモ.
このアイデアと stick breaking-process をくっつけることができる.
GPは基本的には平均関数mに従うので,分散共分散関数由来の,空間的な相関性を持ちながら,
上記のようなガウス分布のかわりを成すことができる.
学習は変分法を導入しており,,これにより高速に計算できる.
わざわざ,うつさないが,パフォーマンスは極めてよいようで,
多手法を圧倒しているようにみえる.
個人的には Gaussian Process と PYPのくっつけ方が実に上手いと思った.
これは,もっと他にも応用の可能性があるのではないかとおもいます.
ちょっと,今日は眠すぎたので,説明がわからなくなってしまった・・・・.
また,気が向いたら,もう少し分かりやすく書きます.ではでは.
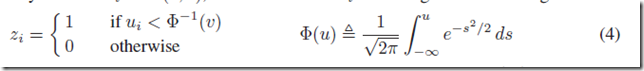

![ビブリオバトル[知的書評合戦]](img/bn_biblio.jpg)

ロレックス時計 使い方 2024-02-11 (sun)
こちらのお店は初めての利用なので、画像だけで判断して注文するのは少し迷いましたが、とても綺麗なダイヤの素敵なネックレスが届きました。
梱包も丁寧で、信頼できるショップだな…と感じました。
また機会がありましたら、よろしくお願いいたします。
ロレックス時計 使い方 https://www.copysale.net/Copy-sale-4433-LOUIS-VUITTON_25E3_2580_2580_25E3_2583_25AB_25E3_2582_25A4_25E3_2583_25B4_25E3_2582_20517760C50.htm
BrandonBrurf 2024-04-20 (sta)
hair falling remedies https://forums.dieviete.lv/profils/127605/forum/ nyc health care