たにちゅーの思惑｜谷口忠大Home Page（たにちゅー・どっと・こむ）

さて，政治×機械学習ネタ第二弾．

今回はもう少し機械学習的には初等的な話！？思いますが・・・

# 第一弾は「ノンパラメトリックな政治家とパラメトリックな専門家」を御覧ください．

 

今回も「こんな考え方あり得るよ」的なおはなしでして，どこの政党がどうであるとか政治批判をする
ような考えは毛頭ございませんので，そういう批判はご勘弁．

また，不謹慎だ！とかいうおはなしも，あくまでクリアな数学のお話ですのでご勘弁．

 

 

さてさて，

政治は政策を立案し，法律を作り，政策を実行するもの
そうなると，
「未来はこうしたい」「こんな日本はいやだ」
みたいな，それぞれの信条というものがあって（ある筈で）
それによって，選挙が行われ候補者から議員が選ばれるわけです．

ただし，現在の民主主義国家では政党制がとられており

僕らは良かれ悪しかれ，議員を選ぶと同時に政党を選ぶことになるわけです．

 

その一方で，政党を選ぶのはそれぞれの議員さんであり，

政党に属していることと，その議員さんの政治的立場と政党の方向性

が大体一緒である事を 僕達としては期待するわけです．

# そうでないと，議員さんを選出してからが不安・・・・

 

 

で，その政党はちゃんと 「同じ考えを持った集団」として出来上がるのでしょうか？

 

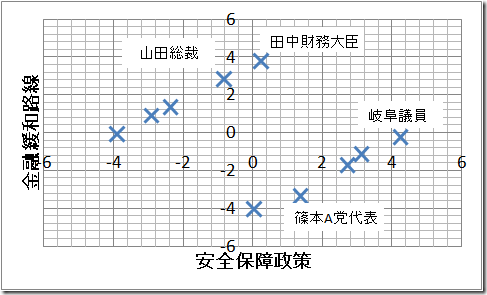
さて，新聞とかを見てると，各政治家の立ち位置を示したイラストがよくあります．

似顔絵つきのんが多いんですが，例えば下のようなやつ（イラストなしですが）

× が各政治家を表します．

 

こう言うのはマーケティングでは知覚マップと呼んだりしますが，

各政治家をいくつかの成分で表現して，それを二次元マップに示すわけです．

# アンケート調査から作ったりしようとすると 主成分分析とか使うと作り易いので

# 覚えておきましょう

 

さて，世は二大政党の時代．

 

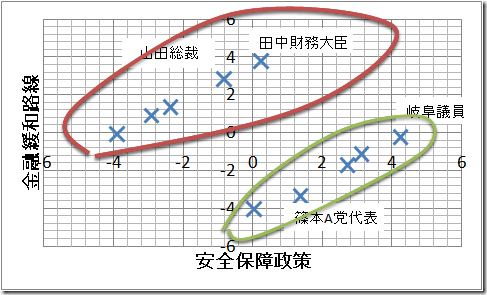
で，上記のようなマップがある場合，

僕らは，二つの政党（勢力）が綺麗にグループ化されていると安心するわけですよねー？

 

で，下のようにグループ化されている事を 勝手に期待する訳なんですね．

 

ところが！！！

 

 

最近の自民党の内部の多様性，民主党のさらなる内部の多様性，内部闘争を見ても

わかるように，必ずしも各政党の中での統一がとれてない！！

 

むしろ，「X議員はむしろ自民党のY議員と近いのでは？なんでわかれてんの？」みたいな

事が往々にしてあるわけです．

 

 

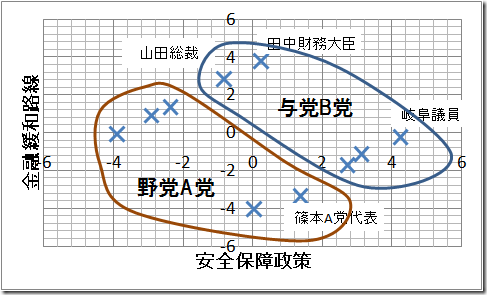
上のマップでも，下のような感じで別れ方がとても微妙なことが，とても多い！！

 

前者のクラスタリングの方が グループ内のまとまりも高く，グループ間の隔たりも大きくて よりよい訳なんですが

どうもそういうふうになってないんですよねー．

 

正直，上の例でもまだましな方で，民主党と自民党の色分けがよくわからないし，

マップ上でも，クラスター自体が重なり合ってるような場合すら見受けられます・・・orz．

 

 

とはいえ，まぁ，とりあえずは上くらいの変なクラスターになっているとしましょう．

国民にとっては，政党内では分裂とかして内部闘争してほしくないので，

上のような政党の別れ方は，なんか気持ち悪いものです．

出来れば始めにしめしたような，すっきりした分かれ方をしてほしい．

 

 

さて，ちゃんとしたグループ化が行われず，こんな微妙なグループ化になぜ

なってしまうんでしょうか？

 

 

「政治家が政局や闘争，既得権益にあぐらをかいて，政策や政治信条ベースで行動してないからだ！」

などと，反射的に批判するひともいますが，

 

実は，これはクラスタリングではよくある話なんですね．

 

こういう，データをグループ分けすることをクラスタリングというのですが，

その代表である k-means法や混合ガウス分布のEMアルゴリズムでは，

こういう局所解に陥ることがしばしばあります．

 

自分が政治家になった時に，どの政党に入るかを決めるのはどうやって決めるでしょうか？

「自分の考えにもっとも近い政党を選ぶ」

のが，妥当かと思います．

 

言い換えれば

「自分の考えと 政党に属している政治家の平均的な考え方 が一番近い政党に属する」

ということではないでしょうか？

 

これは，まさに kmeans法のクラスタリングの方法なんですね．はい．

wikipedia K平均法

クラスタリングの定番アルゴリズム「K-means法」をビジュアライズしてみた …

 

k-means法では，各サンプルを順次，そのサンプルに最も近い平均値を持つクラスターに

割り振っていきます．

これを繰り返すことで，いいかんじのクラスタリングを得ます．

 

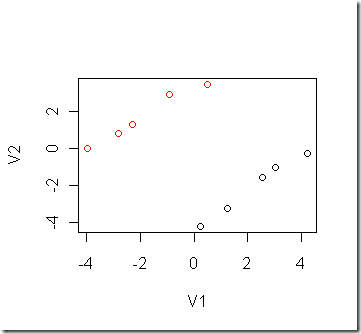
で，kmeans法でクラスタリングしてみると，うまくいくと下記のようになるんですが，

（統計計算ソフトRを利用）

 

実は，kmeans法やEMアルゴリズムといった決定論的なアルゴリズム

「必ず自分の考え（各成分の値：ベクトル値）に一番近い政党（グループ：クラスタ）に所属する」

というやり方では，初期値依存性，局所解というのを持ってしまうと言われています．

 

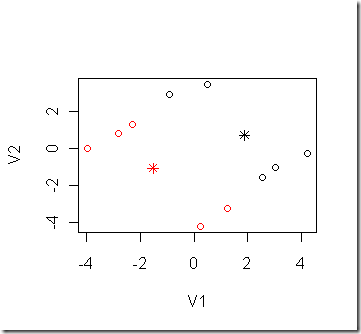
じっさい，kmeans法で何回かやってみると，下のようなベタな局所解がでてきます．

そして，その状態でハマってしまいます．

＊は各グループの平均を 表しているんですが，

 

これは

「自分の考えにもっとも近い政党を選ぶ」

という基準でうまくいっていない政党形成なのでしょうか？

 

いえ，違います．

 

よくみると，ちゃんとどのサンプル点（政治家）も相手のグループの平均より自分のグループの平均の方に

近づいていることがわかるでしょうか？

 

つまり，この状態は安定した状態であり，そういう意味ではキチンとクラスタリングされているのです．

しかし，一番始めに示したような，きれいなクラスタリングにはなっていないんです．

 

 

うーーーーーん

 

 

これは各政治家が真面目に

 

「自分の考えにもっとも近い政党を選ぶ」

ということをちゃんとやっている限り抜け出せない状態なのです！！！

 

 

なんですとっっっっ！！？

 

 

 

つまり，各政治家がちゃんと考えて，決定論的に

「自分の考えにもっとも近い政党を選ぶ」

ことをしていたのでは，一番初めに示したようなきれいなクラスタリングを得られない

事があるのです．

 

ハマってしまう わけですね．

 

 

では，どうすればいいのでしょうか？

 

こういう，惜しい感じのクラスタリングにハマってしまうことを「局所解に陥る」といいますが，

局所解に陥らない探索手法が，存在します．

 

 

たとえば，それは，マルコフ連鎖モンテカルロ法です．

※確率的なので，いつそれを止めるか分からないという意味では，最適でとまれるわけではないが．

 

その 代表例が ギブスサンプラー です．

 

どういうアルゴリズムかというと

各サンプル（政治家）について，各クラスタ（政党）に属する確率（大体距離が近いほど確率大！）を計算します．

 

そして，この確率にしたがって「ランダムに」，どちらかの政党に属するのです．

これを繰り返していくうちに，よりよいクラスタリングが得られていくと考えられます．

詳しくはPRMLとかで勉強しましょう．

# ある意味で大域最適解が保証される．

 

 

つまり，変なクラスタリングに陥っている状態であっても，恐れる事はありません

そこから

一人一人の政治家が，確率的に相手の政党に寝返ることによって，

 

よりまとまりのよい，クラスター（二大政党）が生まれる訳です．

 

ここで，重要なのは，確率的に寝返ることです．決定論的に寝返ってはいけません．

 

でも，メディア的，人道的には「寝返る」なんてもってのほか で，

さらに「確率的に寝返る」なんて，とてもじゃないけど，許されない！って風潮があるようにおもいます．

 

さて，最近，菅政権の下，離党とか引きぬきとかが横行しまくっていて，世も末的な言説も

あるわけでございますが，国民にとっては，内部的に大きなギャップを抱えている政党が支配している

状態は不幸なわけでして，大局的にみると，どんどん寝返ったり，分裂したりしていただいて，

適切な政党集団に組み変わってもらえたほうが，ありがたいという 見方もありえるわけです．

 

 

各政治家が 最適な選択をせずに 確率的に行動するなんて，そんな事が許されてなるものでしょうか！？

 

でも，不思議なことに，各政治家が最適な選択をしている限りは，変なクラスタリング状態，つまり

最適でない解にハマッてしまうということになってしまうわけなのですね．

 

逆に各政治家が常に最適な選択をとるわけではなく，確率的に行動していた方が

全体としては最適なクラスタリング．つまり，二大政党が得られる事があるわけです．

 

ミクロの行動がかならずしもマクロな行動を表象しない，ひとつの例かもしれませんね．

 

 

 

ほかにも，split&merge クラスターを分割したり，併合したりすることを繰り返して最適を目指す

こともありますが，こちらは，「政界再編」のキーワードで呼ばれて，あんまり，メディアでも「悪く」は

言われないですよね～．

 

 

なにをゆーとんのや，この人は？

と思われる方もあるかもしれませんが，

多分，多くの人が，こういう見方をしていた事は無いんじゃないかな？と思うので，

ネタ話までに，書いてみました．

 

 

今度，誰か自民党か民主党の議員が寝返ったり，脱退した場合は

「これも，最適な政党編成へ至るプロセスの一環かもしれない．」

と，大所高所から見る目も数パーセント以下でもいいので，持ってみるのも一興かもしれません．

 

 

 

ちなみに，あなたも何かのグループに属する存在なら

もう少し確率的に行動したほうが世の中のためになるかもしれませんよ！！！？？

 

 

（追伸）

機械学習専門家の皆様による

「階層ベイズでギブスサンプラーでやるとして，ハイパーパラメータどうすんだ！？」 とか

「モデルに特異性ありますよね！？」

のような，話は・・・・ゴニョゴニョ・・・・ということで，場外乱闘でよろしくお願いしますm(_ _)m．