画像特徴量といえば， SIFT，SURF ばかりの単調な僕に李先生が教えてくれました．

「最近，うちはORBばっかりですよ」

なんですと．

Willowgarage が出している descriptor らしい．

よって，当然のようにOpenCVに入っている．

ポイントは，とにかく軽い．バイナリのdescriptor．

論文は

https://willowgarage.com/sites/default/files/orb_final.pdf

なのだが，

この論文がまた，サーベイ的なものがしっかりしていて，また，勉強になる．

頭の良い感じの論文だ．

 

簡単にいうと，

パッチの中にサンプル点をふって そこのintensityを二対比較しまくるという，

なんとも，あっさりとしたもの．

ただ，もちろんrotationやscaleは考慮しないといけないので，そのあたりはやりますよと．

 

 

それでパフォーマンスが出るんですよと．

まぁ，そういうことらしい．

素晴らしい．

 

今年のIROS2012に，RGB-D のバイナリのdescriptorでBRANDって論文が出ていて

現在，某Iくんがラボで実装してくれているのだが，

これは，ORBにとても良く似ていて，それにDepthをORで足し込んだ感じになっている．

 

音の特徴量も，画像の特徴量も，ある種職人芸みたいな世界がつづきますが，

なんとなく，徐々に洗練されている感はありますね．

 

本論文は読んでみるととても良いと思います．

# 最低限のSIFTの知識くらいはあったほうがよいだろうけど．

 

私はそのあたりは完全にユーザなので，適宜使わせていただきます．

arxivからの論文

http://arxiv.org/pdf/1209.5019.pdf

A Bayesian Nonparametric Approach to Image
Super-resolution
Gungor Polatkan, Mingyuan Zhou, Lawrence Carin, David Blei, and Ingrid
Daubechies

 

ノンパラメトリックベイズでは有名な Bleiのグループとの共同研究といった感じでしょうか？

超解像技術（super-resolution）は低解像度画像から高解像度画像を作る技術．

全画素の組み合わせに対して，実際に観測される組み合わせは非常にスパースであることから，

パッチを組み合わせることで，高解像度画像を低解像度画像から復元することができます．

そのためには，辞書(Dictionary)を持つ必要があるのですが，

それをどのように作るかが問題となります．

 

筆者らは過去に

NIPSで

Non-Parametric Bayesian Dictionary Learning for
Sparse Image Representations

http://books.nips.cc/papers/files/nips22/NIPS2009_0190.pdf

を発表しており，ノンパラメトリックベイズを用いて，Dictionary Learning にノンパラメトリックベイズを

応用するということをやっています．

 

それをsuper resolutionに応用するというのが主な筋立てです．

 

基本的にスパースな表現を得る場合には，L1ノルムを用いて刈り込む事が多くて，

超解像でもこれがよく用いられます．

Image Super-Resolution via Sparse Representation
Jianchao Yang et al.

などが良くリファレンスされるらしいです．

 

これに対して，ノンパラメトリックベイズ業界（？）ではスパースな表現にする，

つまり用いない次元を作るような場合には，ベータ・ベルヌーイ分布を導入し，スイッチを作るのが定石です．

 

例えば，

Sharing Features among Dynamical Systems
with Beta Processes

Emily B. Fox et al.

http://videolectures.net/nips09_fox_sfa/

では，HDP-HMM の各隠れ状態に対してストリーム毎にベータ・ベルヌーイのスイッチを設けて，使わない隠れ状態をオフにします．

ちなみに， @k_ishiguro  さんの，

Subset Infinite Relational Models
Katsuhiko Ishiguro et al.

でも，ベータ・ベルヌーイのスイッチをつくって，汎用的な出力分布を用いる（IRMの外に吐き出してしまう）か，

通常のIRMの側に入れるかをえらぶようにしていたりします．

 

というわけで，

「L1刈り込みの代わりを，ノンパラベイズでやるなら，やっぱベータ・ベルヌーイっしょ！」

という，結構ストレートフォワードな適用があるわけです．

 

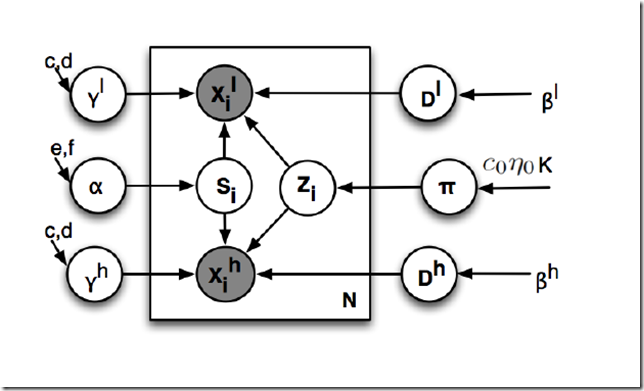
グラフィカルモデルはこんな感じ．

l と h はlow resolution と high resolutionを表している．

xl と xh が観測．

Di と Dh が辞書．

で si が係数なんですが，

zi がいわゆるベータ・ベルヌーイのスイッチで，0,1 をとる．

これによって，使う基底，使わない基底が，0,1でオン・オフされることで，

スパース表現を得るわけである．

なんとも，ストレートフォワードな論理である．

 

ちなみに，これだけでは綺麗にならないみたいで，最後に平滑化処理っぽいことをやる．

 

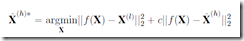
実験の結果は

こんなかんじなのだが，正直，よくわからない・・・．

 

どうも既存手法に勝てているか微妙なのだが，

なるほどな，とおもったのは， Fig.8 で

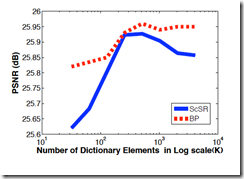
こんな図がある．

これは，辞書の要素数（もとの次元数）を大きくしていった際，BPの場合は打ち切り最大数を大きくしていった時にどうなるか

を示しているのだと思うが，

その時に，ScSR（L1ノルムでのスパースコーディング）はピークを持ってしまう．

これに対しノンパラメトリックベイズのアプローチでは，十分な 要素数があれば，良い値を推定できるので，その良さが維持される．

 

これは，BPのアプローチがもともと無限の状態数を前提として組まれているのに対して，

L1の正則化項は 無次元量でもなく，要素数に影響を受けてしまうからだろう．

 

なるほどねー．

とは思うが，計算量とか考えても，実用的にはL1で行ったほうが，楽で実用的なのかなぁ，と思った次第でございます．

 

本内容は，

Xian-Hua Han (韓 先花） Ph.D にご紹介いただいて (Thank you very much

http://www.iipl.is.ritsumei.ac.jp/XHHan/index.html

それを，僕が勝手に理解したものを書いたものであり，

この記事の内容に誤りがあった場合は，僕を責めてくださいませ．